Hash Tables
GitHub repository link not available yet!
DSA - C implementation of hash tables
Intro
Hash tables are data structures used to store and retrieve values of a certain type under a specific key of a certain type (mostly strings). The reason why they’re called “hash” tables is because they are using hash functions to calculate a numerical index, which is used to access a value from an underlying array. The reason why hash tables are mainly used is because of their speed. In a well-implemented hash table, the time complexity, needed to access an element, can be as little as O(1). Depending on the data, this is the reason why hash tables are used for various map and associative array implementations, indexing and caching.
Hash tables might also have some drawbacks when inefficiently implemented. For example a hash table with a certain hash function might have a higher collision rate than others. This can lead to time intensive lookups.
Implementation
Hash function
For my hash table implementation, I’ve used integers as both keys and values. For both linear probing and chaining hash tables, I’ve used this hash function which is multiplying key value with the large prime number, and then applying modulo with the max integer value. To avoid having number 0 as a valid hash, the number one is added to the resulting hash.
int hash(int key) {
return (key * 2771841997ll) % (2147483647) + 1;
}I am using this function in pair with the function boundedHash, which ensures that the hash value will always be in the range of the array size limit.
int boundedHash(int key, int boundary) {
return hash(key) % boundary;
}Linear probing hash table
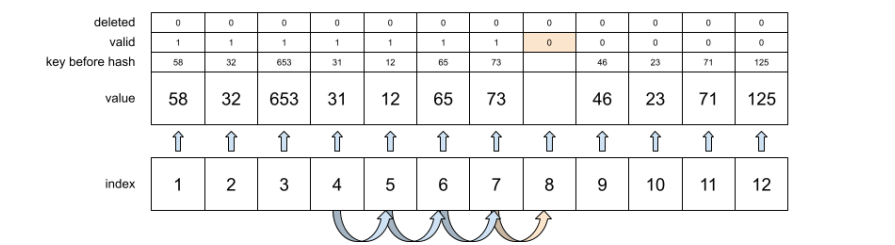
When dealing with the collisions made by hash function, there are several approaches to store values under a certain key, while trying to maintain the short access time. One of the approaches is linear probing. The way linear probing works is that, whenever a collision occurs, the program will try to find the next place in an array which is either empty, or deleted. The structure of this implementation’s main structs is shown in the code below.
// Struct definitions
typedef struct LinearProbingHashItem {
int valid;
int deleted;
int key;
int value;
} LinearProbingHashItem;
typedef struct {
LinearProbingHashItem* table;
int allocated;
int size;
} LinearProbingHashTable;Insert
Implementation of the insert is straightforward. When the function setItem is
called, it is given the key and the value. The first thing which is checked is
whether the hash table has some valid item, and if so, the given value will be
set to this item. Otherwise, the lookup needs to be done. First, appropriate
hash needs to be calculated, and then we will start the lookup process.
Basically, all we’re doing is iterating from the first index which is generated
by our hash function, and we’re checking, whether an item under this key/index
is:
- Either valid
- Its key does not the match the key which was given to the function
- Isn’t deleted
If these three conditions are met, we will just increase the value of our calculated hash, and will continue the lookup. However, if one of these conditions fails, the last iterated item should be the place where we can store the given value. This lookup process looks similar to the picture below.
Before each insert, we also need to check whether we need to resize our table, since its size is limited. The resize function which is implemented, is checking whether the size of the actual items count is less than 80% of the allocated space. If it is, no resize will happen. If the count is however bigger, we will create new instance of a HashTable, with double the size of the allocated space then previous table, we will traverse the first table and clone all of its items to the new table and then we will just assign newly created table to the pointer of an older one.
Search
The search works on a similar principle as insert. When the function getItem
is called, it is given only the key argument, which is hashed into an index and
the resulting hash is used to look for the item which meets all the criteria
mentioned above.
LinearProbingHashItem* getItem(LinearProbingHashTable* ht, int key) {
int hashcode = boundedHash(key, ht->allocated);
while (!(ht->table[hashcode].key == key || ht->table[hashcode].valid == 0 || ht->table[hashcode].deleted == 1)) {
hashcode = (hashcode + 1) % ht->allocated;
}
return &ht->table[hashcode];
}Function returns the reference to the found item.
Delete
All the work delete does, is just finding an item which is valid, based on the key and setting its internal deleted flag to the 1. Therefore, when the setItem function is called, it knows that it can overwrite the value of this item.
void deleteItem(LinearProbingHashTable* ht, int key) {
int hashcode = boundedHash(key, ht->allocated);
while (ht->table[hashcode].key != key) {
hashcode = (hashcode + 1) % ht->allocated;
}
if (ht->table[hashcode].valid == 0) return;
if (ht->table[hashcode].deleted == 0) {
ht->table[hashcode].deleted = 1;
ht->size--;
}
}Benchmarks
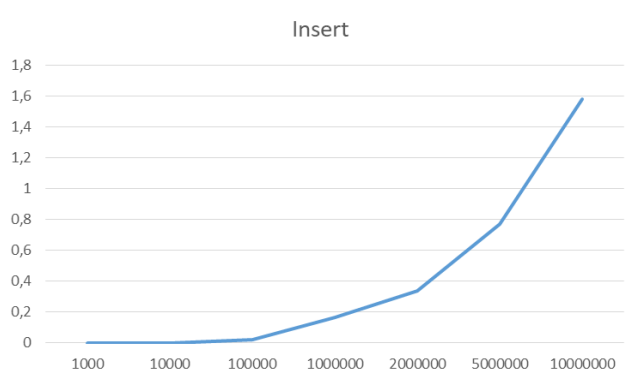
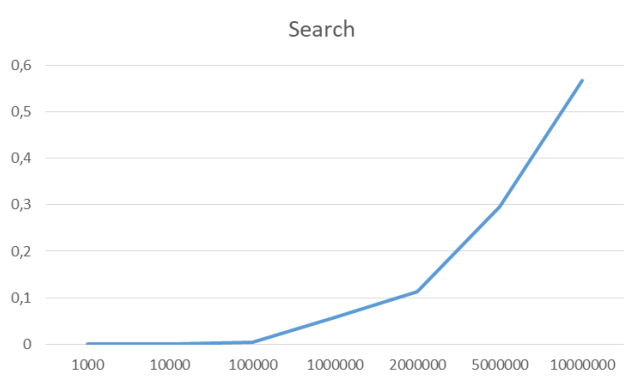
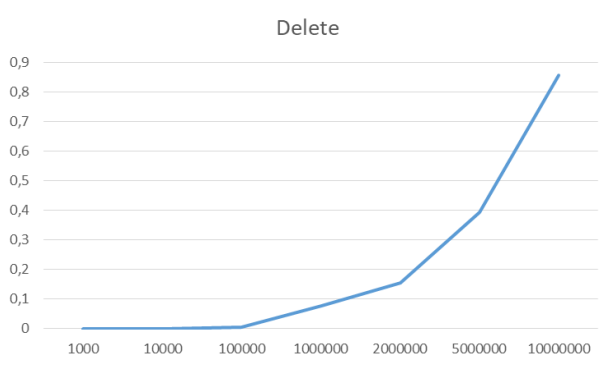
For the benchmarks, I’ve used the data set of n unique unsigned integers.
x-axis: number of elements, on which these implementations were tested
y-axis: time each operation took in seconds.
For testing the speeds, I made this macro to encapsulate the running code, and easily measure the amount of time it took to execute:
#define MEASURE(tag, code) \
{ \
printf("%s ", tag); \
clock_t start = clock(); \
code; \
clock_t end = clock(); \
printf("took %fs\n", (double)(end - start) / CLOCKS_PER_SEC); \
}Here as an example of an actual use of this macro:
MEASURE("Insertion all items", {
for (int i = 0; i < size; i++) {
setItem(&table, dataset[i], dataset[i]);
}
});Insert all items
Search all items
Delete all items
I didn’t include the measurements for elementary operations with a single item, since these all took 0.000 seconds.
Chaining probing hash table
Another approach for maintaining short access time, insertion and deletion, when dealing with collisions, is a method called chaining. The implementation of the chaining hash table is slightly different. Underlying structure is an array of so-called HashItems, where each Hash Item has a pointer to another HashItem, meaning that each item of an array is a linked list. The structure of the table is shown in the image below.
// Struct definitions
typedef struct ChainedHashItem {
int key;
int value;
struct ChainedHashItem* next;
} ChainedHashItem;
typedef struct {
ChainedHashItem** table;
int allocated;
int size;
} ChainedHashTable;Insert
The insert operation works similarly to the way insert works in linear probing hash tables. First we need to check whether the item in the table actually exists. If it does, we can just modify its value and end the function. If it doesn’t, we will calculate the index with our hash function, and check if our table has any item under this index. If it does, we will check whether it’s linked with other HashItems. If it does, we will traverse at the end of this linked list and we will append the newly created HashItem. If it doesn’t, we will just modify the value of it. Similarly to the insert in the linear probing hash table, each insert is also calling the resize function which behaves exactly the same.
Search
When searching an item, we will calculate the index based on our key using our hash function. Then we will use this index to get the HashItem from our table. If null is returned, it means that no value was ever set under this key. However if the HashItem is returned, we need to check if the key of this item matches the key, which was given to this function. If it matches, it means that we found the requested item, but if it doesn’t match, it means that our value is somewhere in the linked list which is in this item. Therefore we need to traverse this linked list, and match every key, and eventually we will find the HashItem for the given key.
Delete
Delete operation is a bit more complicated since manipulating the linked lists is complicated on its own. First things first, we will check whether our hash table does indeed contain items under the given key. If not we will calculate the index, and check if the key, under the found item, does match the given key. If it does, we can move the whole linked list which is linked to this item, to the address of this item, and then we can delete it. This approach will work regardless of whether it has a linked list or not.
In the case of a linked list, we need to traverse it, while maintaining the information about the iterated item, and its parent. If we stumble upon an item, which key matches the given key, we will get the HashItem it is pointing to, and will link it to its parent. This will ensure that we will persist the linked list structure. After this procedure is done, we can delete this item from the memory.
Benchmarks
Insert all items
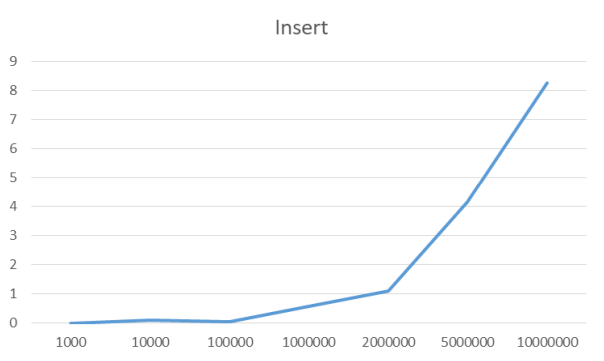
Search all items
404
Couldn't find the chart for this one ._.
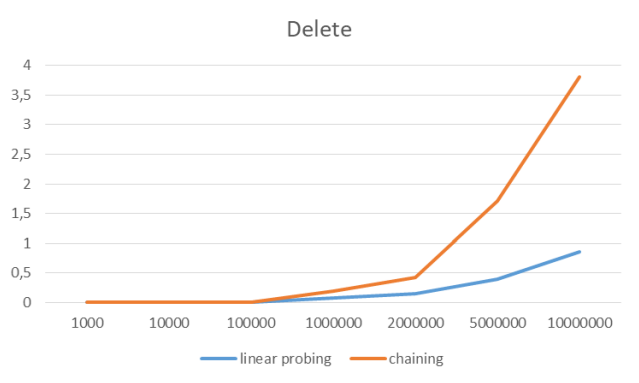
sryDelete all items
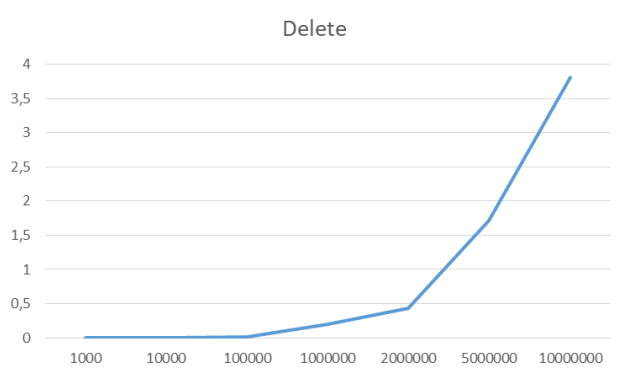
I didn’t include the measurements for elementary operations with a single item, since these all took 0.000 seconds.
Comparison
After measuring elementary operations for both tables, for all elements, we will compare these results.
x-axis: number of elements, on which these implementations were tested
y-axis: time each operation took in seconds.
Insert all items
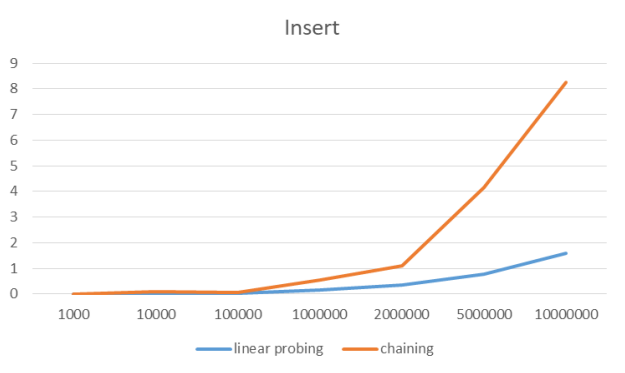
Search all items
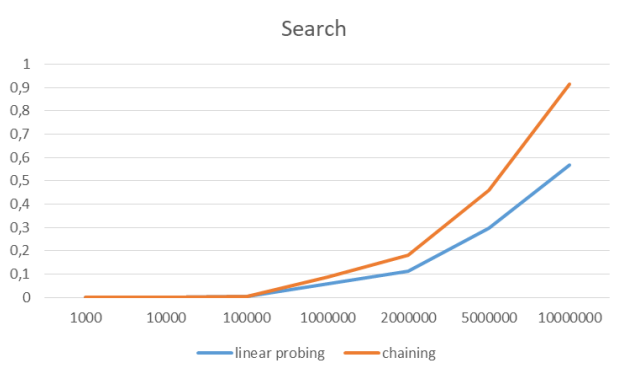
Delete all items
All these measurements were made on my laptop with Intel core i5-5300U and 8 GB DDR3L ram :)